자유 낙하

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 고대 및 중세
- 2.2. 근대 과학 혁명
3. 뉴턴 역학에서의 자유 낙하
4. 일반 상대성이론에서의 자유 낙하
5. 자유 낙하의 응용
6. 한국의 자유낙하 연구 및 활용
참조

1. 개요

자유 낙하는 중력의 영향만 받아 낙하하는 운동을 의미하며, 역사적으로 아리스토텔레스의 무게에 비례한 낙하 속도 주장에 대한 반박과 갈릴레오 갈릴레이의 실험을 통해 이해가 발전했다. 뉴턴 역학에서는 중력 가속도를 사용하여 자유 낙하 운동을 설명하며, 일반 상대성이론에서는 시공간의 측지선을 따라 움직이는 관성계 물체로 정의된다. 자유 낙하는 무중력 상태를 구현하는 데 활용되며, 미소중력 환경을 이용한 신소재 개발, 의학 연구, 우주 개발 등 다양한 분야에서 응용된다.

더 읽어볼만한 페이지

낙하 - 종단속도
유체 속에서 운동하는 물체가 중력과 유체 저항력이 평형을 이루어 더 이상 가속하지 않고 일정한 속도에 도달했을 때의 속도를 종단 속도라고 하며, 이는 물체의 무게와 형태, 유체의 밀도 등에 따라 달라진다.
낙하 - 창밖 투척
창밖 투척은 사람을 창밖으로 던지는 행위를 뜻하며, 프라하에서 발생한 역사적 사건들에서 유래되었고, 정치적·종교적 갈등 상황에서 여러 사례가 나타나며, 대중문화에서도 다양한 방식으로 표현된다.
스카이다이빙 - 스카이서핑
스카이서핑은 1990년대 초에 등장한 익스트림 스포츠로, 낙하산을 이용해 특수 제작된 보드 위에서 자유낙하하며 기술을 선보이는 스포츠이며, 광고 및 ESPN X 게임즈 등을 통해 인기를 얻고 국제항공연맹 공인 세계 선수권 대회도 개최된다.
스카이다이빙 - 베이스 점핑
베이스 점핑은 건물, 안테나, 스팬, 지형 등 고정된 물체에서 낙하산을 이용하여 뛰어내리는 익스트림 스포츠이며, BASE 번호를 부여하고 윙슈트 비행 기술을 활용하며, 관련 법규와 윤리적인 가이드라인 준수가 요구된다.
중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다.
중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.

자유 낙하
개요
자유 낙하 다이어그램. 힘의 균형이 없기 때문에 물체는 아래쪽으로 가속된다.
관련 개념	중력 역학 운동학
상세 정보
설명	자유 낙하는 물체가 중력의 영향만 받는 운동이다.
조건	다른 힘의 부재 (예: 공기 저항, 부력) 균일한 중력장
특징	일정한 가속도 (중력 가속도, 약 9.8 m/s²) 초기 속도 0 (정지 상태에서 낙하) 또는 초기 속도 존재 (던져진 물체의 낙하)
자유 낙하 운동 방정식
변위 (Δy)	Δy = v₀t + (1/2)gt² (v₀: 초기 속도, g: 중력 가속도, t: 시간)
최종 속도 (v)	v = v₀ + gt
속도와 변위의 관계	v² = v₀² + 2gΔy
고려 사항	위 방정식은 이상적인 자유 낙하를 가정한 것이다. 실제 낙하에서는 공기 저항 등의 요인이 작용하여 운동이 달라질 수 있다.
응용
예시	높은 곳에서 떨어지는 물체의 운동 분석 낙하산을 이용한 스포츠 무중력 상태 시뮬레이션
참고	갈릴레오 갈릴레이의 자유 낙하 실험 아이작 뉴턴의 만유인력 법칙

2. 역사

자유 낙하에 대한 개념은 고대부터 존재했지만, 과학적인 이해는 16세기 이후 갈릴레오 갈릴레이 등의 과학자들에 의해 발전되었다.

16세기 이전 서구 세계에서는 일반적으로 낙하하는 물체의 속도가 무게에 비례한다고 가정했다. 즉, 동일한 매질을 통과하는 10kg의 물체는 1kg의 물체보다 10배 빠르게 떨어질 것으로 예상되었다. 고대 그리스 철학자 아리스토텔레스는 역학에 관한 가장 오래된 책 중 하나인 ''물리학''(제7권)에서 낙하하는 물체에 대해 논했다(아리스토텔레스 역학 참조). 그러나 6세기에 요한 필로포누스는 이 주장에 이의를 제기하고 관찰에 따르면 무게가 매우 다른 두 공은 거의 같은 속도로 떨어진다고 말했다.^[1]

12세기 이라크에서 아부 알 바라캇 알 바그다디는 낙하하는 물체의 중력 가속도에 대한 설명을 제시했다. 슬로모 파인즈에 따르면, 알 바그다디의 운동 이론은 "아리스토텔레스의 기본적인 역학 법칙(즉, 일정한 힘은 등속 운동을 생성한다는 법칙)을 부정하는 가장 오래된 것[이며, 따라서 고전 역학의 기본 법칙(즉, 지속적으로 작용하는 힘은 가속도를 생성한다는 법칙)을 모호하게 예측한 것]"이다.^[2]

2. 1. 고대 및 중세

16세기 이전 서구 세계에서는 일반적으로 낙하하는 물체의 속도가 무게에 비례한다고 가정했다. 즉, 동일한 매질을 통과하는 10kg의 물체는 1kg의 물체보다 10배 빠르게 떨어질 것으로 예상되었다. 고대 그리스 철학자 아리스토텔레스(기원전 384~322년)는 역학에 관한 가장 오래된 책 중 하나인 ''물리학''(제7권)에서 낙하하는 물체에 대해 논했다(아리스토텔레스 역학 참조). 그러나 6세기에 요한 필로포누스는 이 주장에 이의를 제기하고 관찰에 따르면 무게가 매우 다른 두 공은 거의 같은 속도로 떨어진다고 말했다.^[1]

12세기 이라크에서 아부 알 바라캇 알 바그다디는 낙하하는 물체의 중력 가속도에 대한 설명을 제시했다. 슬로모 파인즈에 따르면, 알 바그다디의 운동 이론은 "아리스토텔레스의 기본적인 역학 법칙(즉, 일정한 힘은 등속 운동을 생성한다는 법칙)을 부정하는 가장 오래된 것[이며, 따라서 고전 역학의 기본 법칙(즉, 지속적으로 작용하는 힘은 가속도를 생성한다는 법칙)을 모호하게 예측한 것]"이다.^[2]

2. 2. 근대 과학 혁명

아리스토텔레스는 저서 물리학(제7권)에서 낙하하는 물체의 속도가 무게에 비례한다고 주장했다. 즉, 10kg의 물체는 1kg의 물체보다 10배 빠르게 낙하한다고 보았다. 그러나 6세기 요한 필로포누스는 무게가 다른 두 공의 낙하 속도가 거의 같다는 관찰을 통해 이 주장에 이의를 제기했다.^[1]

12세기 이라크의 아부 알 바라캇 알 바그다디는 낙하하는 물체의 중력 가속도에 대한 설명을 제시했다. 슬로모 파인즈에 따르면, 알 바그다디의 운동 이론은 "아리스토텔레스의 기본적인 역학 법칙(일정한 힘은 등속 운동을 생성한다는 법칙)을 부정하는 가장 오래된 것"이며, "고전 역학의 기본 법칙(지속적으로 작용하는 힘은 가속도를 생성한다는 법칙)을 모호하게 예측"한 것이다.^[2]

1589년에서 1592년 사이에 갈릴레오 갈릴레이는 피사의 사탑에서 무게가 다른 두 물체를 떨어뜨리는 실험을 했다고 전해진다. 그러나 낙하 속도를 고려하면, 갈릴레오가 이 실험에서 많은 정보를 얻었을 가능성은 적다. 그는 주로 경사면에서 구르는 물체를 관찰하여 낙하 속도를 늦추고, 물시계와 자신의 맥박을 이용해 시간을 측정했다. 그는 "두 관찰 간의 편차가 맥박의 1/10을 넘지 않을 정도의 정확도"를 얻을 때까지 실험을 반복했다. 같은 시기 갈릴레오는 낙하하는 물체의 운동에 대한 미발표 원고 ''De Motu Antiquiora''를 저술했다.

3. 뉴턴 역학에서의 자유 낙하

뉴턴 역학에서 자유 낙하는 중력 가속도에 의한 등가속도 운동으로 설명된다.

일반적으로 자유낙하운동은 물체가 지표 부근에서 오직 중력만을 받으며 낙하하는 운동을 말한다. 완벽한 자유낙하는 다른 외력이 전혀 존재해서는 안되지만 현실에서는 공기 저항이나 지구의 자전에 의한 관성력과 같은 다른 힘을 받게 된다.^[3] 또한, 엄밀히 말해서 뉴턴의 만유인력을 적용하면 지구의 중력은 지구 중심에서 지표보다 떨어져 있을 경우 중심거리의 제곱에 반비례한다.

: $\mathcal{F} = G {Mm \over r^2}$ G: 만유인력 상수, M : 지구 질량, m : 물체 질량, r : 중심거리

중력 가속도(''g'')는 다음과 같다.

: $g= G{M \over r^2}$

즉, 거리에 따라 가속도 값이 달라진다. 그러나 일반적으로 우리가 관찰하는 물체는 지구 전체 크기로 보았을 때 낙하하고 있다고 해도 거리 변화가 거의 없는 것이나 마찬가지로 가속도 역시 일정하다고 할 수 있다. 지표에서 가속도는

: $g=9.8 \text{m/s}^2 = 32.2 \text{ft/s}^2$

으로 일정하다고 본다.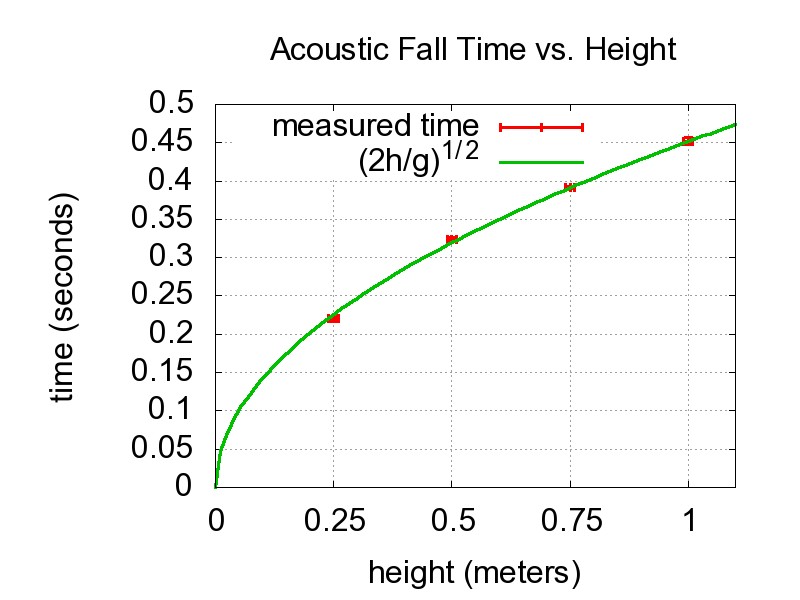

다양한 높이에서 떨어지는 작은 강철 구의 측정된 낙하 시간. 데이터는 $\sqrt{2h/g}$ 의 예측된 낙하 시간과 잘 일치하며, 여기서 h는 높이이고 g는 중력에 의한 자유 낙하 가속도입니다.

지구 표면 근처에서 진공 상태의 자유 낙하 물체는 그 질량과 무관하게 약 9.8m²로 가속된다.

물체는 상승하거나 운동의 정점에서 순간적으로 정지해 있을 때도 기술적으로 자유 낙하 상태에 있다. 중력만이 작용하는 유일한 영향이라면, 가속도^[3]는 항상 아래쪽이며 모든 물체에 대해 같은 크기를 갖는다. 일반적으로

g

로 표시된다. 다른 힘이 없는 경우 모든 물체는 같은 비율로 낙하하기 때문에 물체와 사람은 이러한 상황에서 무중력을 경험한다.

지표면 근처의 충분히 좁은 공간에 있는 물체는, 그 위치에 관계없이 일정한 중력을 받는다고 생각할 수 있다. 이러한 물체의 자유 낙하 운동은, 연직 방향 아래쪽으로 일정한 중력 가속도 ''g''로 가속하는 운동으로 생각할 수 있다.

자유 낙하의 예는 다음과 같다.

추진력이 꺼진 우주선
낙하관 상단에서 떨어뜨린 물체.
위쪽으로 던진 물체 또는 지면에서 낮은 속도로 점프하는 사람

반면, 자유 낙하가 아닌 물체의 예는 다음과 같다.

항공기에서 비행: 양력이라는 추가적인 힘도 있다.
지면에 서 있음: 중력은 지면으로부터의 수직항력에 의해 상쇄된다.
낙하산을 사용하여 지구로 하강: 이때 중력은 공기 역학적 항력과 균형을 이룬다.

1971년 8월 2일, 달에서 우주비행사 데이비드 스콧이 자유 낙하를 실험했다. 그는 달 표면 위 같은 높이에서 망치와 깃털을 동시에 떨어뜨렸다. 망치와 깃털은 같은 비율로 떨어져 동시에 표면에 닿았다. 이것은 공기 저항이 없는 경우 모든 물체가 중력에 의해 같은 가속도를 경험한다는 갈릴레오의 발견을 보여준다. 그러나 달에서는 중력 가속도가 약 1.63m² 또는 지구의 약 ¹⁄₆이다.

3. 1. 공기 저항이 없는 경우

일반적으로 자유낙하운동은 물체가 지표 부근에서 오직 중력만을 받으며 낙하하는 운동을 말한다. 완벽한 자유낙하는 다른 외력이 전혀 존재해서는 안되지만, 현실에서는 공기저항이나 지구의 자전에 의한 관성력과 같은 다른 힘을 받게 된다.^[3]

중력 가속도(''g'')는 지구 표면 근처에서 진공 상태의 자유 낙하 물체가 그 질량과 무관하게 약 9.8m²로 가속되는 것을 의미한다.

지표면 근처의 충분히 좁은 공간에 있는 물체는, 그 위치에 관계없이 일정한 중력을 받는다고 생각할 수 있다. 이러한 물체의 자유 낙하 운동은, 연직 방향 아래쪽으로 일정한 중력 가속도 ''g''로 가속하는 운동으로 생각할 수 있다.

질량을 가진 물체의 속도는 가속도를 시간에 대해 적분한 값으로 구할 수 있다. 이 경우에는 가속도가 상수함수의 꼴이므로 적분하면 다음과 같다.

:

v= v_0 + g t

그러나 초기 속도 v_0가 0임을 고려하면 다음과 같다.

:

v=  g t

가속도를 적분하여 속도를 구했듯이 속도를 적분하면 변위를 구할 수 있다. 처음 변위를

S_0

라 하고 중력 방향을 +로 놓으면, 속도를 시간에 대해 적분했을 때 적분상수는 처음 변위인

S_0

가 되므로 다음과 같다.

:

S = S_0 + {1\over 2} {g t^2}

이는 행성 표면 근처의 작은 거리를 낙하하는 물체의 수직 운동에 대한 "교과서적인" 경우이다. 중력이 공기 저항보다 훨씬 크거나, 또는 동등하게 물체의 속도가 항상 종단 속도보다 훨씬 작은 경우 공기 중에서도 좋은 근사치이다.

:

v(t)=v_{0}-gt\,

:

y(t)=v_{0}t+y_{0}-\frac{1}{2}gt^2

위 식에서 각 문자의 의미는 다음과 같다.

$v_{0}\,$ 는 초기 수직 속도 성분(1m)이다.
$v(t)\,$ 는 시간 $t\,$ 에서의 수직 속도 성분(1m)이다.
$y_{0}\,$ 는 초기 고도(1m)이다.
$y(t)\,$ 는 시간 $t\,$ 에서의 고도(1m)이다.
$t\,$ 는 경과 시간(s)이다.
$g\,$ 는 중력 가속도(지구 표면 근처에서는 9.81m²)이다.

초기 속도가 0이면 초기 위치로부터 낙하한 거리는 경과 시간의 제곱으로 증가한다. 또한, 홀수의 합이 완전 제곱수가 되므로, 연속적인 시간 간격 동안 낙하한 거리는 홀수로 증가한다. 낙하하는 물체의 이러한 거동에 대한 설명은 갈릴레오가 제시했다.^[5]

연직 방향 위쪽으로

z

축을 잡고, 운동을 시작하는 위치를

z=0

으로 한다. 물체를

zx

평면에서 투영각

\theta

, 초속

v_0

로 던져 올린 경우, 속도 및 위치는 진공 중이거나 공기 저항을 무시한 경우 다음과 같다.

속도

:

v_x=v_0\cos\theta

:

v_z=-gt+v_0\sin\theta

위치

:

x=v_0t\cos\theta

:

z=-\frac{1}{2}gt^2+v_0\sin\theta\cdot t

위 식에서 물체의 궤적은 포물선이 된다.^[10]

물체를 초속도 0으로 가만히 낙하시킨 경우의 등가속도 직선 운동은, 이 특수한 경우라고 할 수 있다. 반대로, 포물 운동을 수평 방향의 등속 직선 운동과 자유 낙하(연직 방향의 등가속도 직선 운동)의 합성으로 설명하는 경우도 있다. 이러한 자유 낙하에 관한 사항은 “낙체의 법칙”이라고 불리기도 한다.

3. 2. 공기 저항이 있는 경우

공기 저항을 고려하면 물체는 결국 종단 속도에 도달하게 된다. 이때문에 속도와 위치를 계산하는 식은 더 복잡해진다.^[6]

스카이다이버, 낙하산병 또는 질량 m과 단면적 A를 가진 임의의 물체에 적용되는 경우를 생각해보자. 레이놀즈 수가 임계 레이놀즈 수를 훨씬 상회하여 공기 저항이 낙하 속도 v의 제곱에 비례한다고 가정하면, 운동 방정식은 다음과 같다.

:

m\frac{\mathrm{d}v}{\mathrm{d}t}=mg - \frac{1}{2} \rho C_{\mathrm{D}} A v^2 \, ,

여기서 ρ는 공기 밀도이고,

C_{\mathrm{D}}

는 항력 계수이다. 항력 계수는 일반적으로 레이놀즈 수에 따라 달라지지만 여기서는 상수로 가정한다.

정지 상태에서 낙하를 시작하고 고도에 따른 공기 밀도 변화가 없다고 가정하면, 해는 다음과 같다.

:

v(t) = v_{\infty}\tanh\left(\frac{gt}{v_{\infty}}\right),

여기서 종단 속도는 다음과 같이 주어진다.

:

v_{\infty}=\sqrt{\frac{2mg}{\rho C_D A}} \, .

시간에 따른 물체의 속도를 시간에 대해 적분하면 시간의 함수로서의 수직 위치를 구할 수 있다.

:

y = y_0 - \frac{v_{\infty}^2}{g} \ln \cosh\left(\frac{gt}{v_\infty}\right).

사람의 종단 속도를 56m로 가정하면, 10초 후에는 348미터 낙하하고 종단 속도의 94%에 도달하며, 12초 후에는 455미터 낙하하고 종단 속도의 97%에 도달한다는 것을 알 수 있다. 그러나 고고도에서 낙하하는 물체와 같이 공기 밀도를 일정하다고 가정할 수 없는 경우에는 운동 방정식을 해석적으로 푸는 것이 훨씬 어려워지며, 일반적으로 운동의 수치적 시뮬레이션이 필요하다. 조 키팅거와 펠릭스 바움가르트너의 기록적인 점프는 HALO 점프에 포함된다.^[6]

물체가 대기 중에서 운동하는 경우 공기 저항을 받으므로, 엄밀히 말하면 자유 낙하라고 할 수 없다. 그럼에도 불구하고, 물체의 낙하 운동이 명백히 공기 저항의 영향을 받는 경우에도 자유 낙하라고 부르는 경우가 있다. 낙하하는 물체가 공기 저항을 받는 경우, 공기 저항은 물체의 밀도에 반비례하고, 회전이나 형태, 기류에 따라 다르며, 하부 표면적과 속도에 비례하기 때문에, 무한한 시간이 경과하면 공기 저항과 중력이 균형을 이루어 등속 운동이 된다. 이때의 속도를 종단 속도라고 한다. 물체의 운동 속도가 종단 속도에 비해 충분히 작은 경우, 예를 들어 실험실에서 추의 낙하 운동을 관찰하는 경우 등은 공기 저항을 무시하고 자유 낙하로 생각해도 무방하다.

공기 저항을 받으면서 자유 낙하하는 물체의 낙하 속도 및 위치(고도)는, 낙하 속도를

v_y

, 고도를

y

라고 하면 다음과 같다. 단, 낙하 속도와 고도 모두 수직 상방향을 양으로 한다.

:

\begin{align}ma_{y} &= -kv_y - mg \\v_y &= \left(v_{y0} + \frac{m}{k}g \right) e^{-kt/m} - \frac{m}{k}g \\y &= -\frac{m}{k} \left[ \left( v_{y0} + \frac{m}{k}g \right) \left( e^{-kt/m}-1 \right) + gt \right] + y_0\end{align}

y_0

는 물체의 초기 고도,

v_{y0}

는 초속도,

m

은 질량,

k

는 공기 저항 계수이다.

종단 속도

v_{y\infty}

는

v_y

의 극한을 취함으로써 구할 수 있다.

:

v_{y\infty}=\lim_{t \to \infty}v_y = - \frac{m}{k}g

3. 3. 만유인력의 법칙

일반적으로 자유 낙하 운동은 물체가 지표 부근에서 중력만을 받으며 낙하하는 운동을 말한다. 두 물체가 다른 힘이 없는 공간에서 서로를 공전하는 경우, 서로를 중심으로 자유 낙하하는 것으로 볼 수 있다. 예를 들어, 달이나 인공위성이 지구 주위를 공전하거나, 행성이 태양 주위를 공전하는 경우를 들 수 있다. 구형 물체라고 가정하면, 운동 방정식은 만유인력의 법칙에 의해 지배되며, 중력 2체 문제의 해는 케플러 법칙을 따르는 타원 궤도가 된다.^[7] 지구 근처의 낙하하는 물체와 공전하는 물체 사이의 관계는 뉴턴의 대포알이라는 사고 실험으로 가장 잘 설명된다.

아이작 뉴턴(Isaac Newton)은 달이 왜 지표면에 떨어지지 않는가 하는 의문에 대해, 달은 지구를 향해 계속 낙하하고 있다고 답했다. 이러한 천체의 운동도 중력(만유인력)의 영향만을 받는 운동이므로 자유 낙하이다. 물론 이것은 지구에도 해당되는 것으로, 지구는 항상 태양을 향해 계속 낙하하고 있다는 것이 된다. 또한, 중력은 한쪽이 다른 한쪽을 일방적으로 끌어당기는 힘이 아니라, 상호적으로 끌어당기는 힘이다. 따라서 지구도 또한 달을 향해 낙하하고 있다는 것이 된다. 다만, 달보다 지구의 질량이 크기 때문에, 지구가 달을 끌어당기는 요소가 상대적으로 크다.

4. 일반 상대성이론에서의 자유 낙하

일반 상대성이론에서 자유 낙하는 힘을 받지 않는 물체가 측지선을 따라 움직이는 관성계 운동이다. 시공간 곡률의 근원으로부터 멀리 떨어져 시공간이 평평한 곳에서는 뉴턴의 자유 낙하 이론이 일반 상대성이론과 일치한다. 그렇지 않으면 두 이론은 일치하지 않는다. 예를 들어, 일반 상대성이론만이 궤도의 세차 운동, 중력파로 인한 밀집 쌍성의 궤도 붕괴 또는 나선형 접근, 그리고 방향의 상대성(측지선 세차 운동 및 틀끌림)을 설명할 수 있다.^[1]

갈릴레오가 주목하고 뉴턴의 이론에서 중력 질량과 관성 질량의 동일성으로 구현되었으며, 이후 현대적인 형태의 에트뵈시 실험에 의해 높은 정확도로 확인된, 모든 자유 낙하하는 물체가 같은 비율로 가속된다는 실험적 관측은 등가 원리의 기초이며, 아인슈타인의 일반 상대성이론이 처음으로 출발한 기반이다.^[1]

5. 자유 낙하의 응용

자유 낙하는 중력 외에 다른 힘의 영향을 받지 않는 이상적인 상태를 의미한다. 이러한 조건에서는 모든 물체가 질량에 관계없이 동일한 가속도로 낙하한다. 지구 표면 근처에서 진공 상태의 물체는 약 9.8 m/s²의 가속도를 갖는다.

자유 낙하의 예시로는 추진이 중단된 우주선, 낙하관에서 떨어지는 물체, 위로 던져진 물체 등이 있다. 1971년, 데이비드 스콧은 달에서 망치와 깃털을 동시에 낙하시키는 실험을 통해 공기 저항이 없을 때 모든 물체가 같은 가속도로 떨어진다는 사실을 입증했다.^[3]

그러나 현실에서는 공기 저항으로 인해 물체는 종단 속도에 도달한다. 스카이다이버의 경우 종단 속도는 대략 53 m/s (190 km/h 또는 118 mph)이다.^[4]

물체가 상승하거나 운동의 정점에 순간적으로 정지해 있는 경우도 엄밀히 말하면 자유 낙하 상태이다. 이때 중력만이 유일한 영향력으로 작용하며, 가속도는 항상 아래쪽을 향하고 모든 물체에서 동일한 크기(일반적으로 g로 표시)를 갖는다.

5. 1. 미소중력 실험

자유 낙하를 통해 미소중력 상태를 만들 수 있다. 이는 이상적인 무중력 상태와는 다르지만, 실제로는 미소중력 환경을 구현하는 효과적인 방법이다. 인류는 낙하탑, 항공기, 우주선 등을 이용하여 미소중력을 얻고 있다. 국제우주정거장도 미소중력 환경에서의 연구를 위한 시설 중 하나이다.^[3]

미소중력 상태에서는 물과 기름처럼 지상에서 섞이지 않는 물질들이 분리되지 않고 혼합된다. 이러한 특성은 신소재 개발에 활용된다. 또한, 단백질 등의 결정이 지상보다 더 크고 쉽게 성장하기 때문에 의학 연구에도 이용된다. 우주선 내부에서는 장기간 미소중력 상태를 유지할 수 있으므로, 생물이 장기간 또는 여러 세대에 걸쳐 미소중력에 노출되었을 때의 영향을 연구하는 데 사용된다. 이러한 연구는 미래 인류의 장기간 우주 활동을 염두에 둔 것이다.

5. 2. 놀이기구

자이언트 드롭과 같은 프리폴 놀이기구는 낙하하는 스릴과 낙하 시의 무중력 상태를 즐기기 위한 놀이기구이다.^[3]

5. 3. 우주 개발

국제우주정거장을 비롯한 우주 시설은 자유 낙하를 통해 장기간 미소중력 환경을 유지한다. 이러한 환경은 지상에서는 섞이지 않는 물질들이 균일하게 혼합되는 특성을 이용하여 신소재 개발에 활용된다.^[1] 또한, 단백질 결정이 지상보다 크고 쉽게 성장하는 환경은 의료 연구에 이용된다.^[1]

우주선 내부는 장기간 미소중력 상태를 유지할 수 있어, 생물이 장기간 또는 여러 세대에 걸쳐 미소중력에 노출되었을 때의 영향을 연구하는 데 사용된다.^[1] 이는 인류의 장기 우주 활동을 염두에 둔 연구이다.^[1]

6. 한국의 자유낙하 연구 및 활용

한국은 전통적으로 자유 낙하에 대한 과학적 이해가 부족했으나, 근대화 이후 서구 과학의 영향을 받아 자유 낙하 연구가 발전하였다.

참조

_[1] 서적 A Source Book in Greek Science Harvard University Press
_[2] 백과사전 Abu'l-Barakāt al-Baghdādī , Hibat Allah Charles Scribner's Sons
_[3] 웹사이트 The Feynman Lectures on Physics Vol. I Ch. 8: Motion https://www.feynmanl[...]
_[4] 웹사이트 Free fall graph http://www.greenharb[...] Green Harbor Publications 2010-03-14
_[5] 서적 The Mechanical Universe: Introduction to Mechanics and Heat https://books.google[...] Cambridge University Press
_[6] 학술지 High altitude free fall http://www.jasoncant[...]
_[7] 학술지 From Cavitation to Astrophysics: Explicit Solution of the Spherical Collapse Equation https://link.aps.org[...] 2024-06-07
_[8] 학술지 From Moon-fall to motions under inverse square laws
_[9] 학술지 Radial Motion of Two Mutually Attracting Particles https://apps.dtic.mi[...]
_[10] 웹사이트 https://wakariyasui.[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com